| Theorem 1 |
 |
|
Any transposition changes the inversion parity
of a given permutation
|
Proof: It is not difficult to see
that the transposition of neighboring elements, 
and 
, changes the inversion parity of a
given permutation.
The transposition of any elements, 
and 
, can be expressed as the sequence
of (2k-1)
transpositions.
Really, by k transpositions of the element
with the neighboring element from the
right of 
. we get the permutation 
:
.
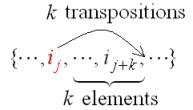Then, by k - 1
transpositions of the element 
with the neighboring element from the
left of 
, we get the desired permutation 
:
Thus, the whole number of the transpositions k+k-1=2k-1 is an odd number, Hence, the theorem.
| Theorem 2 |
|
Given the set  , there are n!
different permutations of S |
Proof: Consider an arbitrary permutation of S.
The first position can be displaced by any of n elements.
The second position can be displaced by any of the rest n - 1 elements.
The third position can be displaced by any of the rest n - 2 elements, and so on.
The n-th position can be displaced by the rest single element.
Therefore, there are n(n - 1)(n - 2)...1 = n! ways to get a new permutation of elements of S.
