A normal vector to a plane is a perpendicular vector to the plane.

According to geometrical postulates,

• A point and a vector determine a plane.
• Three points determine a plane.

The general equation of a plane in a rectangular Cartesian coordinate system has the following form:

,

(*)

where x, y and z are running coordinates of a point in the plane.

Let be a point in the plane, that is,

.

(**)

Combining equation (*) with identity (**) we obtain another form of the general equation of a plane:

.

(***)

Assume that A, B and C are coordinates of some vector n. Then the sum on the left hand side of equation (***) is the scalar product of the vectors n and r-r1:

.

By the properties of the scalar product this equality implies that the vector n is perpendicular to the vector r-r1. Since r-r1is an arbitrary vector in the plane P, n is a normal vector to the plane P.

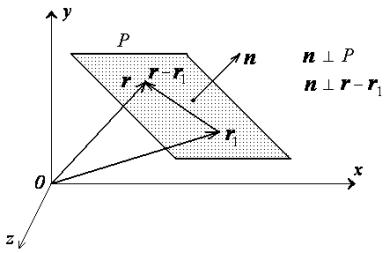
Thus, equation (***) describes a plane that passes through the point , and the coefficients A, B and C can be interpreted as the coordinates of a normal vector to the plane.

Consider a few particular cases of equation (*).

1. If D = 0 then the plane

passes through the origin.

2. If C = 0 then the plane

is parallel to the z-axis.

3. If B = 0 then the plane

is parallel to the y-axis.

4. If A = 0 then the plane

extends along the x-axis.

5. If A = B = 0 then the plane

is parallel to the x, y-plane, that is, the plane is perpendicular to the z-axis.

In a similar way we can interpret another cases.