Аргументация. Предположим, что  n  элементов нужно разместить в  n  ячейках.

Первый элемент можно случайным образом поместить в любую из  n  ячеек.

Для каждого из  n  вариантов размещения первого элемента существует (n – 1) способ размещения второго элемента – в любую из оставшихся ячеек.

Третий  элемент можно поместить в любую из (n – 2) свободных ячеек и т.д.

Полное число способов случайного размещения  n  элементов по  n  ячейкам равно

n (n – 1) (n – 2) … 1 = n!

Комментарии. С равным успехом мы могли бы говорить о числе способов извлечения случайным образом  n  шаров из ящика с  n  шарами (в схеме без возвращения шаров).

При первом извлечении можно достать любой из  n  шаров.

При втором извлечении можно достать любой из оставшихся (n – 1) шаров и т.д.

Полное число способов извлечения  n  шаров из ящика, содержащего  n шаров, (без возвращения шаров) равно  n (n – 1) (n – 2) … 1 = n!

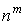Аргументация. При первом извлечении можно достать любой из  n  шаров.

После возвращения шара на место число шаров в ящике вновь становится равным  n. Поэтому при каждом последующем извлечении можно достать любой из  n  шаров.

.

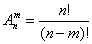Аргументация. Доводы те же, что и в п. 1).

Единственное отличие заключается в том, что число элементов  m  меньше числа ячеек и поэтому последний  m^ый элемент можно поместить в любую из оставшихся  (n – m + 1) ячеек.

Следовательно,

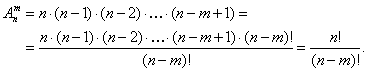
Эквивалентная формулировка. Число способов извлечения случайным образом  m  шаров из  ящика, содержащего  n  шаров, в схеме с упорядочиванием без возвращения шаров равно

.

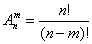Например, из первых пяти цифр можно составить

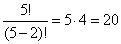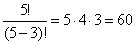          различных двузначных чисел,

          различных трехзначных чисел,

         или  5! = 120 различных пятизначных чисел.