Пример 3.  Игральная кость подбрасывается 1 раз.

Событие A:  Выпадение на верхней грани числа очков большего 2.

Решение. Число возможных исходов равно 6: выпадение 1, 2, …, 6 очков.

Число исходов, благоприятствующих событию A, равно 4: выпадение 3, 4, 5 или 6 очков.

.

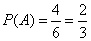Пример 4.  Игральная кость подбрасывается 2 раза.

Событие A:  Сумма выпавших очков – четное число.

Событие B:  Сумма выпавших очков равна 6.

Событие C:  Грань, содержащая 1, не выпала ни разу.

Событие D:  Грань, содержащая 1, выпала оба раза.

Решение. Число возможных исходов равно 6²=36.

(A)   Событие  A  разлагается на 18 исходов:

-        При первом и втором подбрасываниях выпали четные числа очков, что приводит к 3 · 3 = 9  исходам.

-        При первом и втором подбрасываниях выпали нечетные числа очков, что также приводит к 3 · 3 = 9  исходам.

.

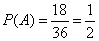(B)   Событие  B  разлагается на 5 исходов:

(1, 5),  (2, 4),  (3, 3),  (4, 2),  (5, 1).

.

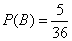(C)   При одном подбрасывании кости в 5 из 6 случаев происходит выпадение какого-то числа очков кроме 1.

При двух подбрасываниях кости в  5² = 25  из  6² = 36  случаев происходит выпадение каких-то чисел очков кроме 1.

.

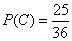(D)   При одном подбрасывании кости в 1 из 6 случаев происходит выпадение 1.

При двух подбрасываниях кости в  1  из  36  случаев происходит выпадение 1.

.

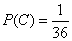Пример 5.  Игральная кость подбрасывается 6 раз.

Событие A:  Грань, содержащая 1, выпала хотя бы один раз.

Решение.  Рассмотрим противоположное событие B:  Грань, содержащая 1, не выпала ни разу при шести подбрасываниях кости.

Вероятность P(B) такого события (т.е. вероятность выпадения каких-то чисел очков кроме 1) равна  (5/6)⁶.

Однако события A и B вместе образуют достоверное событие: какое-то из них обязательно произошло – либо 1 не выпала ни разу, либо 1 выпала хотя бы один раз.

Следовательно,  P(A) + P(B) =1, что влечет за собой

.