|
|
| Как рассуждал Даламбер ... |
|
|
|
|
|
Пример 1. Правильная монета подбрасывается 2 раза. Событие A: Выпадение хотя бы одного “орла”. Решение. Число возможных исходов в серии из двух испытаний равно 4: ОО, ОР, РО, РР.
Число исходов, благоприятствующих событию A, равно 3: ОО, ОР, РО. Следовательно,
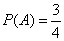 . .Пример 2. В семье имеется 2 ребенка. Событие A: Хотя бы один из детей – мальчик. Решение. Задача по своей сути не отличается от предыдущей. Только под испытанием теперь следует понимать рождение ребенка. Если рождение мальчика или девочки в одном испытании представляют собой случайные события, то число равновероятных исходов равно 4: ММ, МД, ДМ, ДД. Только первые 3 исхода благоприятствуют событию A. Поэтому
Ошибочное решение. Число возможных вариантов в серии из двух испытаний равно 3: ММ, МД, ДД. Первые два исхода благоприятствуют событию A. Поэтому 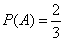 . .Анализ. Три события:
“2 мальчика”,
“1 мальчик и одна девочка” и
“2 девочки”
не являются равновозможными, поскольку ММ и ДД представляют собой элементарные события, тогда как событие “1 мальчик и одна девочка” – составное событие, которое разлагается на 2 исхода: МД и ДМ. Любопытно, что подобную ошибку в рассуждениях допустил в свое время великий математик Даламбер, рассматривая задачу о подбрасывании монеты (см. Пример 1). |
|
|