Рассмотрим функцию δ (x, γ) колоколообразного типа, зависящую от параметра γ
и удовлетворяющую условию
| |
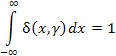 
|
(1) |
|
при любых (достаточно малых) значениях параметра γ.
Предположим, что при убывании γ график этой функции вытягивается вдоль оси 0y и одновременно
сжимается, как это показано на рисунке.
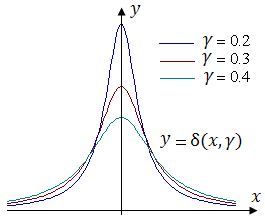
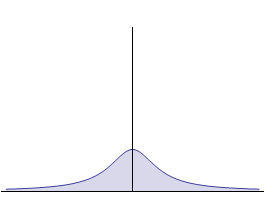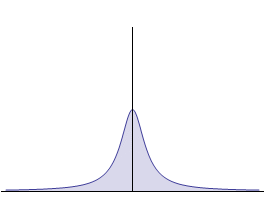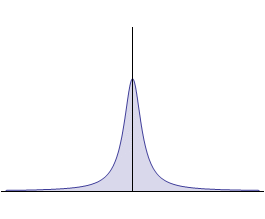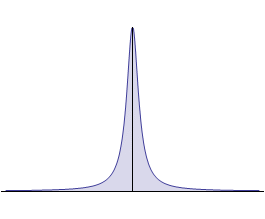
В результате предельного перехода γ → 0 функция δ (x, γ)
преобразуется в дельта-функцию Дирака δ (x):
| |
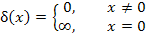 
|
(2) |
|
При этом
| |
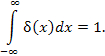 
|
(3) |
|
В некотором смысле дельта-функция представляет собой обобщение дельта-символа Кронекера, определяемого условиями
| |
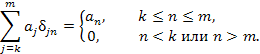 
|
(4) |
|
Очевидно, что дельта-функция является четной функцией,
δ (– x) = δ ( x), 
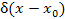 равна нулю за пределами ε-окрестности точки
x0. Поэтому равна нулю за пределами ε-окрестности точки
x0. Поэтому
|