|
Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1). 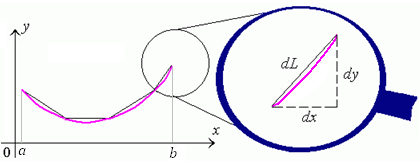
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком. Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
Длина дуги равна сумме длин составляющих ее элементов:
|

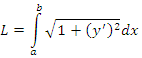 .
.