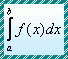| Introduction |
Basic Conceptions
| First-Order Differential Equations |
Directly Integrable Equations
Motion of a Body - Problem 1
Motion of a Body - Problem 2
Motion of a Body - Problem 3
The Spontaneous Radioactive of Substance
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Separable Equations
Motion of Particals in Viscous Fluid
Newton's Model of Cooling
Model of Population
Homogeneous Equations
Linear Equations
Bernoulli Equations
Exact Differential Equations
| Differential Equations of Higher Orders |
Basic Conceptions
Equations of Special Kinds
Some Graphic Illustrations using MATLAB
| Real-Life Problems:
Newton's Model of Cooling |
Let the temperature of some body at time t be T(t), and let the ambient temperature have a time independent value A.
- Assume that T(0) = T0
> A.
Then the cooling of a body can be described by Newton's Model of Cooling, which states that the time rate of change of the temperature is proportional to the difference between temperatures:The value of the proportionality constant k is determined by the properties of the object and ambient. However, in any circumstances > 0. .
.
Separation of variables and integration gives the general integral of the differential equation:
Since T(0) = T0 then .
and so
.
and so .
Therefore,
.
Therefore, .
which yields the particular solution:
.
which yields the particular solution: .
.
One can see that T(t) approaches the limit A as .
.
 .
.
- Let us assume now that T0
< A.
Then the heating of a body is described by the following initial value problem:
In a similar way as above we obtain the particular solution, which obeys the initial condition: .
.
 .
.
 .
.
|
|