Принцип Гамильтона   
       Одно из наиболее важных приложений уравнений Эйлера связано с их применением для решения задач классической механики, электроднамики и квантовой физики.

       Положение точки в пространстве описывается ее радиус-вектором  r, координатами которого являются декартовы координаты  x, y, z  точки. Система, включающая в себя  N  частиц, имеет  3N  степеней свободы и для определения положений всех ее частиц необходимо задать  3N  координат.

       Наряду с декартовой системой координат используются и дргие системы. Оптимальный выбор системы координат определяется спецификой решаемой задачи, в частности, свойствами симметрии. Поэтому роль некоторых координат частиц могут выполнять, например, угловые переменные. Поэтому любые величины, характеризующие положение системы, называют ее обобщенными координатами и обозначают их символами  q1,  q2, ...,  qn, где  n  – число степеней свободы системы.

       В любой момент времени конфигурация системы определяется значениями обобщенных координат  q1,  q2, ...,  qn, совокупность которых можно рассматривать в качестве координат точки в  n-мерном пространстве конфигураций. При этом каждой конфигурации системы соответствует определенная точка.

       В процессе эволюции системы точка конфигурационного пространства описывает некоторую кривую, которую условно можно назвать "траекторией движения системы". Другими словами, движению системы можно поставить в соответствие траекторию точки в пространстве конфигураций. Любая точка такой траектории в пространстве конфигураций изображает всю систему в некоторый момент времени.

       Производные 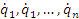   по времени  t  от обобщенных координат называются обобщенными скоростями системы. Одновременное задание координат и скоростей частиц однозначно определяет положение и эволюцию системы.

       Любая механическая система характеризуется функцией Лагранжа 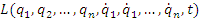 , которая представляет собой разность между кинетической и потенциальной энергиями системы:

L = T – V.

       Пусть в моменты времени  t1  и  t2  система занимает некоторые положения, каждому из которых соответствует определенная точка в пространстве конфигураций.
       Определим функционал  S  (называемый действием) уравнением

       Принцип Гамильтона устанавливает, что для консервативных систем переход из одной точки конфигурационного пространства в другую происходит таким образом, что функционал  S  (то есть действие) принимает наименьшее значение. (Точнее сказать – экстремальное значение).
       По этой причине принцип Гамильтона называют также принципом наименьшего действия.