|
Определение. Пусть 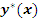 – экстремаль функционала – экстремаль функционала  , то есть , то есть 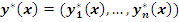 удовлетворяет системе уравнений Эйлера удовлетворяет системе уравнений Эйлера

Функция 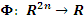 называется первым интегралом системы уравнений Эйлера, если называется первым интегралом системы уравнений Эйлера, если
| |
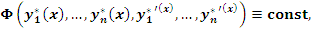
|
(1) |
|
то есть функция  сохраняет постоянное значение на любом решении системы уравнений Эйлера. сохраняет постоянное значение на любом решении системы уравнений Эйлера.
Пример первого интеграла дает следующая теорема.
Теорема 1. Если функция F не зависит явно от x, то её первым интегралом является функция Гамильтона H, определяемая равенством
| |
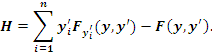
|
(2) |
|
Доказательство. Используя семейство преобразований 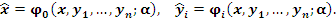 и учитывая
Предложение 1, и учитывая
Предложение 1,
Предложение 1:
Пусть семейство преобразований 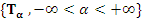 задается равенством
и функция 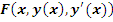 не зависит явно от х.
Тогда функционал
инвариантен относительно семейства преобразований 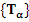 .
|
получаем
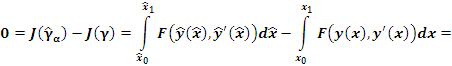
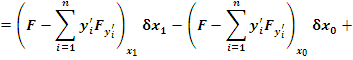
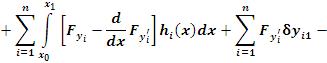

Если  – экстремаль, то есть является решением системы уравнений Эйлера, то – экстремаль, то есть является решением системы уравнений Эйлера, то
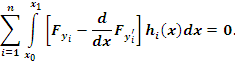
Далее имеем
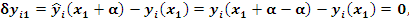
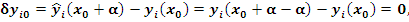
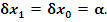
Используя эти равенства, получаем
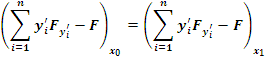
В силу произвольности выбора точек 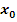 и и 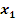 отсюда следует, что отсюда следует, что
| |
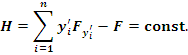
|
(3) |
|
Теорема доказана.
|