Элементы функционального анализа   
       При изучении этой темы предполагается, что студенты знакомы с элементами функционального анализа, именно - с основными типами функциональных пространств (метрическими, банаховыми, гильбертовыми) и теорией линейных операторов.

       Напомним некоторые понятия из функционального анализа, которые будут использоваться в последующем изложении.

       Определение 1. Множество  Е  называется линейным нормировнным пространством над полем вещественных или комплексных чисел, если

  1. Е  - векторное пространство над полем вещественных (комплексных) чисел;


  2. на  Е  задана норма, то есть функция  || · || :  Е → R, которая каждому элементу  x ∈ Е ставит в соответствие число ||x||, причем
    a)  ||x|| ≥ 0  для всех  x ∈ Е  и  ||x|| = 0  тогда и только тогда, когда  x = 0;
    б)  ||λ x|| = |λ| ||x||  для каждого  λ  из поля скаляров и каждого  x ∈ Е;
    в)   ||x + y|| ≤ ||x|| + ||y||.
       Линейное нормированное пространство является метрическим с метрикой  р (х, у) = ||x – y||.

       Определение 2. Линейное нормированное пространство  Е  называется банаховым, если оно является полным относительно метрики  р (х, у) = ||x – y||, то есть каждая фундаментальная последовательность  хn  (||хn –хm||→ 0 при  n,m → ∞) сходится к некоторому элементу из  Е.

       Примеры

  1. Пространство  С[a, b]  - множество непрерывных функций  f : [a, b] → R  с нормой  ||f|| = maxa ≤ t ≤ b |f (t)|.


  2. Пространство  C(p)[a, b] - множество функций  f : [a, b] → R, имеющих непрерывные производные до p-го порядка включительно с нормой

       Определение 3. Функционал - это числовая функция  Φ(x), заданная на банаховом пространстве  E.
       В дальнейшем будут рассматриваться функционалы с действительными значениями. На функционалы распространяются обычные понятия анализа: непрерывность, дифференцируемость и другие.

       Определение 4. Функционал  Φ : E → R называется непрерывным в точке  y0 ∈ E, если для любого  ε > 0  существует  δ > 0, что для всех  y  таких, что  ||y - y0|| < δ, выполняется неравенство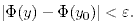

       Определение 5. Функционал  l( · ) : E → R  на банаховом пространстве  E  называется линейным, если

1)   l (λ1 y1 + λ2 y2 )   = λ1 l (y1) +  λ2 l (y2),

2)   l ( · )  - непрерывен.

       Определение 6. Функционал  Φ(y), определенный на банаховом пространстве  E, называется дифференцируемым в точке  y0 ∈ E, если приращение  ∆Φ(y0, h) ≡ Φ(y0 + h) - Φ(y0) представимо в виде:

 ∆Φ(y0, h) = l (h) + o(h),

где  l (h)  - линейный функционал,  o(h) = α(h) · ||h||, причем  α(h) → 0 при  ||h|| → 0.

       Линейный функционал  l (h)  обозначается  δΦ(y0, h) и называется первой вариацией функционала  Φ  в точке  y0 ∈ E.

       Определение 7. Точка  y0 ∈ E  называется точкой локального максимума (минимума) функционала  Φ( · ) :  E → R, если существует окрестность  U (y0) = {y ∈ E :||y — y0|| < ε} ,  ε > 0, точки  y0  такая, что для всех  y ∈ U(y0)  выполняется неравенство  Φ(y) < Φ(y0) (соответственно  Φ(y) > Φ(y0)).
       Если выполняется строгое неравенство, то точка  y0  называется точкой строгого локального максимума (минимума).
       При нахождении локальных экстремумов дифференцируемых функционалов используется следующий результат (аналог известной в анализе теоремы Ферма).

       Утверждение. Если функционал  Φ :  E → R  дифференцируем в точке  y0 ∈ E  и  y0  является точкой локального экстремума, то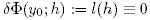

для всех  h ∈ E.

       Доказательство: Пусть, например,  y0  - точка локального минимума.
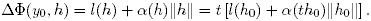
       Предположим, что существует элемент  h0 ∈ E, для которого  l (h0) ≠ 0, скажем  l (h0) > 0.
       Полагая  h = t h0,  t  - вещественное число, рассмотрим приращение


       Для достаточно малых  t  выражение в скобках будет положительным, а поэтому  ∆Φ(y0, h) > 0  при  t > 0  для сколь угодно близких к  y0  точек из  E.
       Это противоречит тому, что  y0  является точкой локального максимума.
       Утверждение доказано.