|
Матрица первого порядка содержит единственный элемент, и этот элемент является определителем матрицы.
Рассмотрим квадратную матрицу второго порядка,
| |
 . .
|
(1) |
|
Для вычисления определителя матрицы A нужно рассмотреть все возможные перестановки индексов, нумерующих ее столбцы. В рассматриваемом случае перечень возможных перестановок множества {1, 2} исчерпывается двумя вариантами:
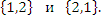
Перестановка {1, 2} не содержит инверсий и поэтому является четной, тогда как перестановка {2, 1} является нечетной, ибо содержит одну инверсию.
Эти перестановки порождают произведения

алгебраическая сумма которых представляет собой определитель матрицы второго порядка:
| |
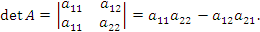
|
(2) |
|
В случае матрицы третьего порядка существует уже шесть различных перестановок множества
{1, 2, 3}:
{1, 2, 3}, {2, 3, 1}, {3, 1, 2},
{3, 2, 1}, {2, 1, 3}, {1, 3, 2}.
Первые три перестановки являются четными, поскольку каждая из них содержит четное число инверсий. Оставшиеся три перестановки являются нечетными, так как каждая из них содержит нечетное число инверсий (см Примеры).
Таким образом,
Эту формулу можно легко запомнить с помощью правила треугольников, которое иллюстрируется представленными ниже рисунками.

Рис. 1. Произведения элементов, расположенных на главной диагонали матрицы или в вершинах треугольников, основания которых параллельны этой диагонали, берутся со своими знаками.

Рис. 2. Произведения элементов, расположенных на побочной диагонали матрицы или в вершинах треугольников, основания которых параллельны этой диагонали, берутся с противоположными знаками.
|