В качестве определения единичной матрицы могло бы выступать примерно такое.
Матрица E называется единичной, если при умножении на нее любой матрицы A (слева и справа) матрица A остается неизменной: AE = EA = A.
Оказывается, что элементы единичной матрицы описываются ранее введенным выражением δi j.
Разумеется, что такое утверждение о структуре единичной матрицы требует проверки. И следует позаботиться о соответствующем обобщении понятия единичного элемента в матричной алгебре - по сравнению с обычной единицей в системе чисел.
Связано это с тем, что операция умножения определена не для любых матриц и, следовательно, требуется определенное согласование размеров иатриц-сомножителей. В результате под единичной матрицей понимается матрица вышеуказанной структуры, порядок которой выбирается таким, чтобы соответствующее произведение было определено.
 ), называется единичной матрицей и обозначается символом E.
), называется единичной матрицей и обозначается символом E.
 .
.
 .
.
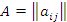 – произвольная матрица размера m×n. Рассмотрим i,j-ый элемент матричного произведения AE, где E – единичная матрица n-го порядка.
– произвольная матрица размера m×n. Рассмотрим i,j-ый элемент матричного произведения AE, где E – единичная матрица n-го порядка.

