Примеры матриц:
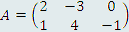 ,
, 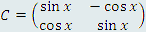 .
.
Матричный элемент, расположенный на пересечении i-ой строки и j-го столбца, записывается в виде ai j , а выражение A = || ai j || означает, что матрица A составлена из элементов ai j :
 .
.
|
|
| Понятие матрицы |
|
|
|
|
|
Матрица представляет собой прямоугольную таблицу элементов, в качестве которых могут выступать числа, функции, символы, слова и так далее - при условии, что заданы определенные правила математических действий с этими элементами.
Примеры матриц: 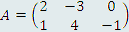 , , 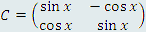 . .
Матричный элемент, расположенный на пересечении i-ой строки и j-го столбца, записывается в виде ai j , а выражение A = || ai j || означает, что матрица A составлена из элементов ai j :  . .
|
||||
|
Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции.
Матричная алгебра имеет обширные применения в различных отраслях знания – в математике, физике, информатике, экономике. Например, матрицы используется для решения систем алгебраических и дифференциальных уравнений, нахождения значений физических величин в квантовой теории, шифрования сообщений в Интернете. Матрица обозначается одной из заглавных букв латинского алфавита, а набор ее элементов помещается в круглые скобки:
Матрица  размера n×1
называется столбцевой или вектор-столбцом. Для краткости вектор-строку и вектор-столбец обычно называют просто векторами. размера n×1
называется столбцевой или вектор-столбцом. Для краткости вектор-строку и вектор-столбец обычно называют просто векторами.
Особую роль играют матрицы, у которых число строк совпадает с числом столбцов, то есть матрицы размера n×n. Такие матрицы называются квадратными При ссылке на квадратную матрицу достаточно указать ее порядок. Например, матрица третьего порядка имеет размер 3×3. Квадратная матрица порядка 1 отождествляется с единственным ее элементом.
|
||||
|
|